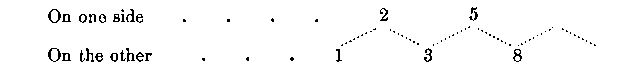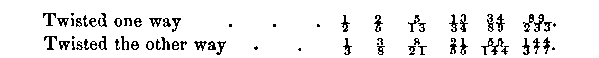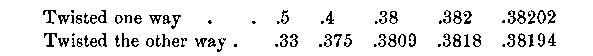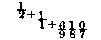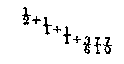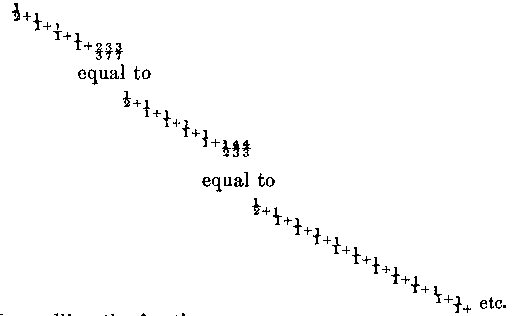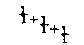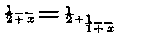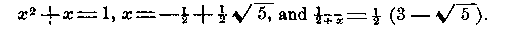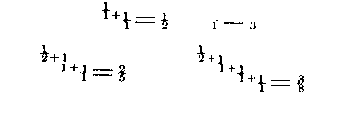A Popular Explanation (For those who Understand Botany) of the Mathematical Nature of Phyllotaxis [From American Naturalist 10 (June 1876): 326-329. Published by Harvard Botany professor George Goodale.] ⁴⁸

BY THE LATE CHAUNCY WRIGHT. This article was prepared by Mr. Wright several years ago, at Professor Gray's suggestion. In its manuscript form it has been found of much interest and value to the botanical students in Harvard College. It is here reprinted without change from Mr. Wright's notes. ⁴⁹

Take, by the finger and thumb of your right hand, hold of a spike of Plantago major, Lepidium Virginicum, or other flower-cluster with symmetrically crowded flowers, and with the finger and thumb of the left hand grasp it a little higher up, so as to include between the two hands a dozen or twenty buds on a piece of stem about equally tough from end to end. Twist the stem, and if it twists equally in all parts you will bring your buds into a small number of ranks, let us say 8. By twisting a little in the opposite direction you will get them into 5 ranks. Twist harder, and if your stem is tough enough to stand the twist you will bring them into two ranks. Turn back to 8 rows, and twist harder in that direction; you will fetch your buds into 3 rows. Then twist still harder in that direction, and if you have an old, tough, plaintain spike, you may get the seed-vessels all into one row before your stalk is twisted off.

Thus by mechanical twisting, if the twist is equal in all parts of the stem, we get on one side of the natural position the number of rows 5 and 2, and on the other side 8, 3, and 1. Hence if we begin with the most twisted position and come toward the natural position, we get the numbers

Now these series of numbers indicate the approach towards the untwisted position. What would be the number of ranks in that theoretically perfect untwisted state? As both these series of numbers are increasing, that is, the number of ranks decreases as you twist either way, you may infer that in the untwisted state the number of ranks is prodigious or innumerable. Carrying on the series by adding zigzag as the lines are dotted, we should get

Hence we say that the slightest conceivable twist in one direction makes the number of ranks 377, a little more in that direction gives 144, 55, 21, 8, 3, 1, while the slightest twist in the opposite direction gives us 233, a little more 89, 34, 13, 5, 2, 1.

There is, however, a mystery in the space between 233 and 377, between twisting one way and twisting the other. Let us not seek to solve it by running the number of ranks up higher, to 610, 987, 1597, etc., but approach it in another way.

In the stem twisted one way, the angle between the leaves is 1/2 the whole circumference, or or 2/5, or 5/13, etc.; with the stem twisted the other way the angle is or 1/3, or 3/8, or 8/21, or 21/55 etc., the circumference. Let us set these in double rows: —

Or putting them in decimals we shall see how they converge towards the same value: —

Take the high fraction 1597/4181 in the upper series and turn it into decimals, we get .38196603. If the leaves were at this angle they would form 4181 rows or ranks, and the least twist would produce the lower numbers. Let us now attempt to find some

simpler mode of representing these fractions .38196608 or 1597/4181, which are the same.

Dividing both numerator and denominator of 1597/4181 by 1597 will give 1/2 + 987/1597; dividing each term of the last fraction by 987 gives us

and continuing the process gives us

equal to

Now calling the fraction

continued indefinitely by the name of x, it is plain that the phyllotactic fractions beginning with 1/2, 1/3, 2/5, 3/8, 5/13 continually approach nearer and nearer to the value 1/2+x or

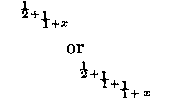
whence

This expression, 1/2 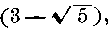is equal to .38196+, and expresses the exact ratio of the leaves in a theoretically untwisted stem when the number of rows is infinite. Other arrangements

are simply approximations to this (as though they aimed at this but got the stem twisted in growing), such as