The most thorough Uniform Distribution of Points about an Axis. [From Runkle's Mathematical Monthly 1.7 (April 1859): 244-248.] ⁷

ByChauncey Wright, Nautical Almanac Office, Cambridge, Mass.

Let it be required to place at equal successive intervals round and round upon the circumference of a circle, an indefinite number of points, so that the circumference shall at any time be divided by them into the smallest parts; that is, so that the circumference shall be most thoroughly divided at every step of the distribution.

If we were not limited to equal intervals between the successive points, the distribution might be very simply effected either by continually bisecting or trisecting the parts of the circumference. Thus two points placed oppositely would divide the circumference into two equal parts, and with two other points these semi-circumferences might be bisected, according to the arrangement of cruciform flowers

and whorls; and further, four more points might bisect the quadrants, and so on. Or, again, the circumference might at first be divided by three points into three equal parts, and these might be bisected or trisected by the three or six following points, and so on.

To divide the parts of the circumference into smaller fractions than thirds would be to neglect the distribution at first, though the ultimate division of the circumference would be quite as perfect But if now we seek a uniform and symmetrical distribution as well as a thorough one, the interval between the successive points must be constant, and if the circumference is to be indefinitely subdivided, this interval is of course incommensurate.

Let x denote the ratio of this interval to the whole circumference; then 1/x is the number of times the interval is contained in the whole circumference. Let q denote the integer part of 1/x and r' the remainder after subtracting q x from the whole circumference.

In the second revolution around the circumference each of the parts x is divided into the parts r' and x - r' . In the third revolution each of the parts x - r' into the parts r' and x - 2 r' , and so on as many times as r is contained in x. Let this number be q', and let the remainder, x - q' r' , be denoted by r''.

By further revolutions each of the intervals r' is subdivided into q″ parts r'' with a third remainder r'''; and so on. The numbers and spaces q, q', q'', &c., r', r'', r''' &c., are such as are obtained by the method for finding the greatest common divisor or for forming a continued fraction, and since

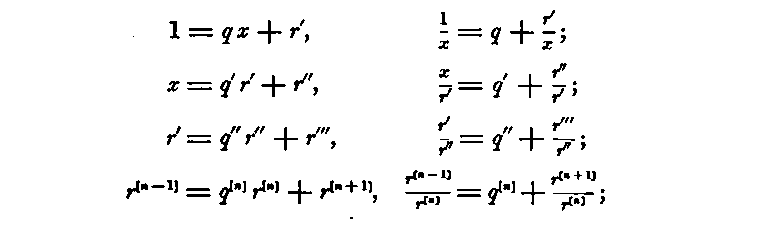
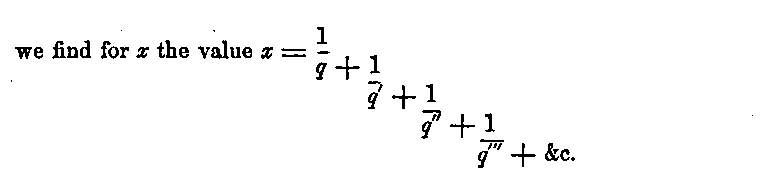
Now in order that the circumference may be at every step most thoroughly divided, the magnitudes of the parts into which it is divided should be as nearly equal as possible; that is, the smaller should be contained in the larger the least number of times; hence, in general, the numbers q[n], which express the ratios of successive sub-intervals, should be unity. It may not be necessary that the distribution should begin till after the first revolution. In this case the first quotient q may be any number, but all the other quotients, q', q'', q''', &c., must be unity, hence

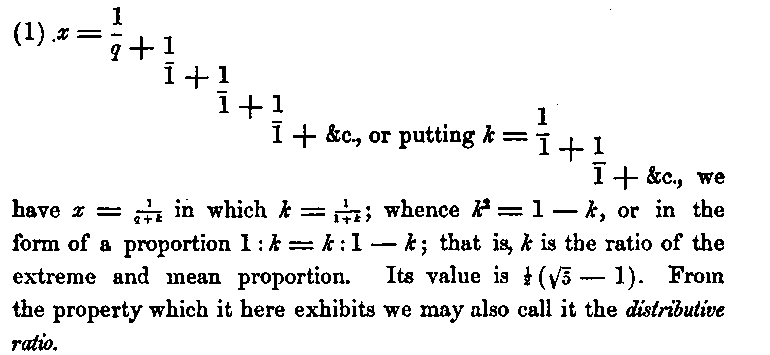
This ratio k and the continued fraction, which expresses it, have hitherto been obtained by mathematical induction from the fractions of the Phyllotaxis. On the other hand we shall be able by further deductions, still subject to the conditions of our problem, to obtain these fractions as special solutions. For, in cases where the circumference is to be divided into a limited number of parts, the interval

x becomes commensurate, and the last remainder or space of the foregoing analysis is contained exactly twice in the last but one; that is, the last step of the distribution consists in bisecting the previous parts of the circumference. ' Or, what comes to the same, the last remainder but one is contained in the preceding remainder once, with a remainder equal to itself, so that the last two remainders are equal. Hence, for a distributive commensurate interval, all the values q[n] are unity, but are limited in number; and the interval is therefore one of the approximations of the continued fraction (1).

When q = 1 these approximations are 1, 1/2, 2/3, 3/5, 5/8, &c. When q = 2 they are 1/2, 1/3, 2/5, 3/8, &c., the arithmetical complements of the former, and they therefore express the same arrangements, but in an opposite direction around the circumference. When q = 3 we obtain 1/3, 1/4, 3/7, &c.

In general the third approximation

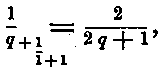
or two divided by any odd number, expresses the intervals which, in the second revolution, are bisected. The fractions 2/3, 2/5, and 2/7 are the only ones of this simplest form of distribution which are found in the arrangements of leaves around their stems. In all the arrangements of the Phyllotaxis every point after the first revolution is so placed with reference to the two points, between which it falls, that its distance from the middle is never more than one sixth of the whole interval between the two points. The distributive property of these fractions clearly explains their office in nature.

Many other fractions are apparently as well adapted to the symmetry of vegetable forms, and the limitation of natural arrangements to the Phyllotactic system seems, therefore, at first sight, unaccountable. Two hypotheses have been advanced to explain this limitation; the one attempting to deduce these arrangements mechanically from a hypothetical law of formation; and the other

regarding them as typical forms or models which nature has chosen to follow by an arbitrary limitation of her means. The latter hypothesis certainly agrees best with the principles of animal and vegetable Morphology, according to which organized forms are not determined simply by their functions, but are rather certain typical structures or models, modified and metamorphosed by their functions.

There are three ways in which we may seek to account for natural forms and phenomena. First, by deducing them from the law. of their development, as in the mechanical sciences; or, secondly, we may account for them by the discovery of their functions or offices as in Physiology; or, thirdly, by referring them to fundamental types or natural methods, as in the Morphology of organized forms. To the latter class of explanations belongs the most generally received account of the Phyllotaxis; that is, the arrangements of this system are regarded as the models by which nature works, and not as the result of any discoverable law of formation, nor as performing any special function in the vegetable economy. But we have shown that there is a purpose which these arrangements fulfil, and that no other arrangements are adapted to the same office. This office in plants is to effect the most thorough distribution of leaves and petals around their axes; to expose them most effectively to the influences of light and air, and to distribute their fibres most thoroughly in the stem. Thus the functions of leaves and petals determine not only their general forms, but also in general their relative positions. Expansion and exposure are the conditions required by the functions, and the Phyllotaxis is only a simple mathematical deduction from these conditions.