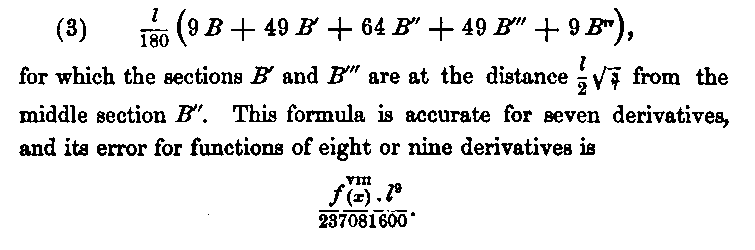Extension of the Prismoidal Formula.6
BY CHAUNCEY WRIGHT
We have shown that the Prismoidal Formula is an exact definite integral for algebraic expressions of positive integer powers not exceeding the third degree, and that it is sufficiently accurate in all cases where the fourth order of differences may be neglected. We propose now to determine similar formulas, which shall include higher orders of differences.
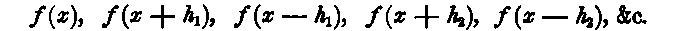
a series of sections made perpendicular to the axis of X, through a solid or plane figure, and at the distances x, x + h1, x - h1, &c. from the origin of x, then the expression
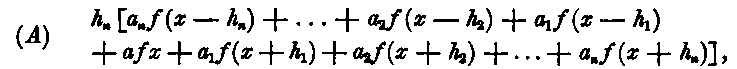
which contains 2 n + 1 terms, n + 1 coefficients a, a1, a2, &c., and n values h1, h2, &c., may be made to represent the contents of any portion of the solid or plane figure for which f(x) is an algebraic expression of positive integer powers not exceeding the (4 n — l)th degree.
Formula (A) may be written thus: —
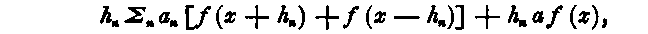
and developed by Taylor’s Theorem, it becomes
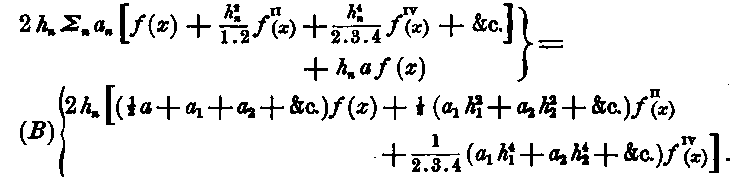
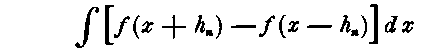
becomes, when developed,
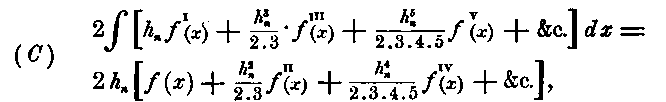
and, if we make the corresponding terms of (B) and (C) equal, we have the following equations
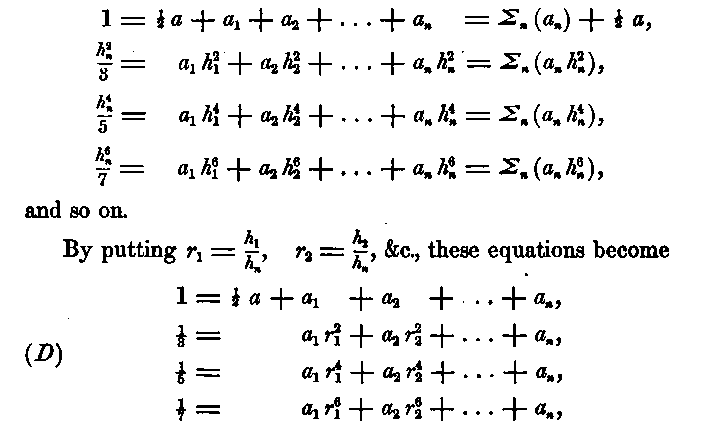
and so on, in which a, a1, a2, &c., are the coefficients of the sections, and r1, r2, &c., the ratios of their distances from the middle section to the distance A, of the extreme sections from the middle.
If by l we denote the whole distance between the extreme sections, then hn = l/2.
The number of the equations (D) which can be satisfied is equal to the number of undetermined quantities a, a1, a2, ...an; r1, r2, ... rn-1, that is, to (n + 1) + (n - 1) = 2 n. But the (2 n + 1)th
terms of the expressions (B) and (C) contain the coefficients of the 4nth derivative of f(x), which are therefore the first not included in the equations (D); hence (-4) may be made accurate for (4 n — 1) derivatives of f(x). When the sections are made at equal intervals, the distances h1, h2, &c., and the ratios r1, r2, &c., are determined by their number, and (A) can be made accurate only for as many derivatives of f(x) as there are sections, that is, for 2 n + 1. Since there are 2 n equations (D) the last will be of the form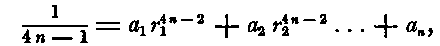
and the error of (A) for functions of two higher orders of derivatives, that is for functions which have 4 n, or 4 n + 1 derivatives, is
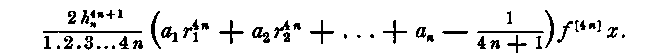
EXAMPLES.
1. When there are only three sections, n = 1, and the equations (D) become 1 = 1/2 a + a1 and 1/3 = a1, hence a = 4/3 and (A)
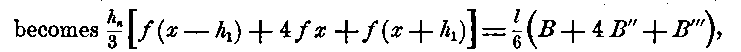
which is the common prismoidal formula.
2. When n = 2, there are five sections, and the equations (D) become
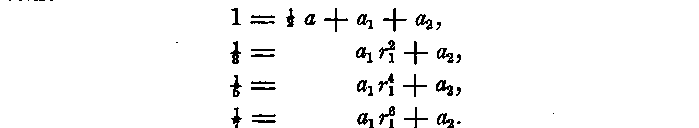
If these sections are made at equal intervals, then r1 is determined, and only three of these equations can be satisfied; that is, only five orders of derivatives can be included by them. As the second and fourth sections will in this case bisect the intervals between the middle and the extreme sections, r1 = 1/2 and the equations
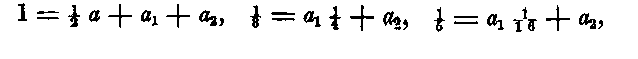
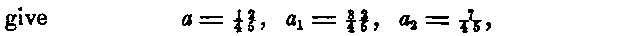
so that the formula (A) becomes
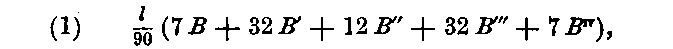
and its error for functions of six or seven derivatives is
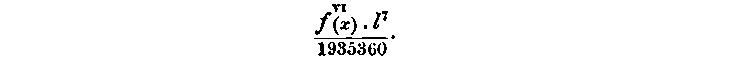
If r1 be taken so that the coefficient a of the middle section shall disappear, then
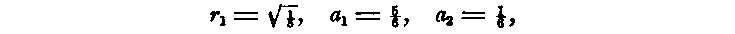
and we obtain a formula of four sections,
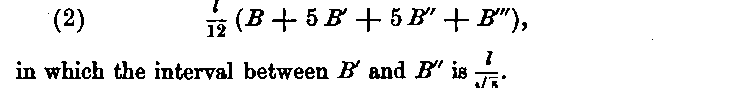
This formula is accurate for five derivatives, and its error for functions of six or seven derivatives is
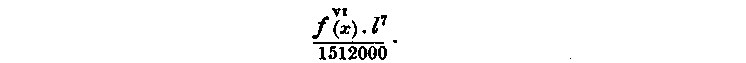
If r1 is left indeterminate, then the solution of the four equations above will give
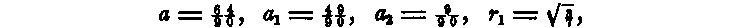
and we obtain the formula of five sections
This error and those of formulas (1) and (2) may be estimated in terms of the finite differences of f(x) by the following transformations. If the length l be divided by sections into so many parts m that the corresponding differences of f(x) of a higher order than the ith, may be neglected, then
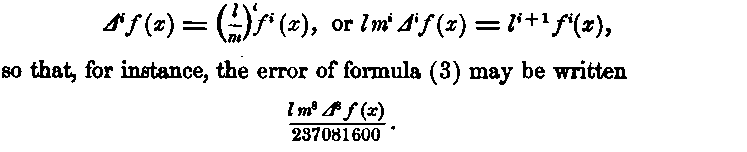
Hence, if the number of parts m into which l is divided be about the eighth root of 237081600, or about 11, and if the corresponding value of Δ8f(x) be inappreciable, then formula (3) is sufficiently accurate. In the same way the accuracy of formulas (1) and (2) may be estimated in practice.
In the application of formulas (1), (2), and (3) to symmetrical figures, as for instance for determining the contents of casks, since the sections at equal distances from the middle section are equal, these formulas may be written thus: —
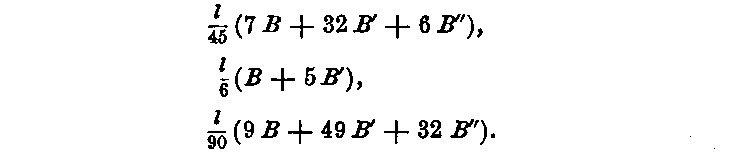
Cases in practice might arise in which sections at equal intervals could not be obtained. For such cases special formulas might be easily obtained from the equations (D).
In some future number of this journal we shall apply the formulas of the preceding discussion to a variety of problems in Engineering, Tonnage of Vessels, Cask Gauging, &c.